Odredite vrijednost funkcije u tački ekstrema. Ekstremum funkcije dvije varijable. Primjeri proučavanja funkcija za ekstrem. Fizičko značenje izvedenice

Okrenimo se grafu funkcije y = x 3 - 3x 2. Razmotrimo susjedstvo tačke x = 0, tj. neki interval koji sadrži ovu tačku. Logično je da postoji takva okolina tačke x = 0 da funkcija y = x 3 - 3x 2 zauzima najveću vrijednost u ovom susjedstvu u tački x = 0. Na primjer, na intervalu (- 1; 1) najveća vrijednost jednaka 0, funkcija zauzima u tački x = 0. Tačka x = 0 naziva se maksimalna tačka ove funkcije.

Slično tome, tačka x = 2 naziva se minimalna tačka funkcije x 3 - 3x 2, jer u ovom trenutku vrijednost funkcije nije veća od njene vrijednosti u drugoj tački u blizini tačke x = 2 , na primjer, susjedstvo (1,5; 2,5).

Dakle, tačka x 0 naziva se maksimalna tačka funkcije f (x) ako postoji okolina tačke x 0 - takva da je nejednakost f (x) ≤ f (x 0) zadovoljena za sve x iz ovog susjedstvo.

Na primjer, tačka x 0 = 0 je maksimalna tačka funkcije f (x) = 1 - x 2, budući da je f (0) = 1 i nejednakost f (x) ≤ 1 istinita za sve vrijednosti od x.

Minimalna tačka funkcije f (x) naziva se tačka x 0 ako postoji takva okolina tačke x 0 da je nejednakost f (x) ≥ f (x 0) zadovoljena za sve x iz ove okoline.

Na primjer, tačka x 0 \u003d 2 je minimalna tačka funkcije f (x) = 3 + (x - 2) 2, budući da je f (2) = 3 i f (x) ≥ 3 za sve x .

Ekstremne tačke se nazivaju minimalne i maksimalne tačke.

Okrenimo se funkciji f(x), koja je definirana u nekom susjedstvu tačke x 0 i ima izvod u ovoj tački.

Ako je x 0 tačka ekstrema diferencijabilne funkcije f (x), tada je f "(x 0) \u003d 0. Ova izjava se naziva Fermatov teorem.

Fermatova teorema ima jasno geometrijsko značenje: u tački ekstrema, tangenta je paralelna sa x-osi i stoga njen nagib
f "(x 0) je nula.

Na primjer, funkcija f (x) \u003d 1 - 3x 2 ima maksimum u tački x 0 = 0, njen izvod f "(x) = -2x, f "(0) = 0.

Funkcija f (x) = (x - 2) 2 + 3 ima minimum u tački x 0 \u003d 2, f "(x) = 2 (x - 2), f "(2) = 0 .

Imajte na umu da ako je f "(x 0) \u003d 0, onda to nije dovoljno da se tvrdi da je x 0 nužno tačka ekstrema funkcije f (x).

Na primjer, ako je f (x) = x 3, onda je f "(0) = 0. Međutim, točka x = 0 nije tačka ekstrema, budući da se funkcija x 3 povećava na cijeloj realnoj osi.

Dakle, tačke ekstrema diferencijabilne funkcije moraju se tražiti samo među korijenima jednačine
f "(x) \u003d 0, ali korijen ove jednadžbe nije uvijek tačka ekstrema.

Stacionarne tačke su tačke u kojima je derivacija funkcije jednaka nuli.

Dakle, da bi tačka x 0 bila tačka ekstrema, neophodno je da bude stacionarna tačka.

Uzmite dovoljne uslove da stacionarna tačka bude tačka ekstrema, tj. uslovi pod kojima je stacionarna tačka minimalna ili maksimalna tačka funkcije.

Ako je derivacija lijevo od stacionarne tačke pozitivna, a desno negativna, tj. derivacija mijenja znak "+" u znak "-" kada prolazi kroz ovu tačku, tada je ta stacionarna tačka maksimalna tačka.

Zaista, u ovom slučaju, lijevo od stacionarne tačke, funkcija raste, a desno se smanjuje, tj. ova tačka je maksimalna tačka.

Ako derivacija promijeni znak "-" u znak "+" kada prolazi kroz stacionarnu tačku, tada je ta stacionarna tačka minimalna tačka.

Ako derivacija ne promijeni predznak pri prolasku kroz stacionarnu tačku, tj. derivacija je pozitivna ili negativna lijevo i desno od stacionarne tačke, tada ova tačka nije tačka ekstrema.

Razmotrimo jedan od zadataka. Pronađite ekstremne tačke funkcije f (x) = x 4 - 4x 3.

Rješenje.

1) Pronađite izvod: f "(x) = 4x 3 - 12x 2 = 4x 2 (x - 3).

2) Pronađite stacionarne tačke: 4x 2 (x - 3) \u003d 0, x 1 \u003d 0, x 2 = 3.

3) Koristeći metodu intervala, utvrđujemo da je izvod f "(x) \u003d 4x 2 (x - 3) pozitivan za x\u003e 3, negativan za x< 0 и при 0 < х < 3.

4) Budući da se prilikom prolaska kroz tačku x 1 \u003d 0, predznak derivacije ne mijenja, ova tačka nije tačka ekstrema.

5) Derivat mijenja znak "-" u znak "+" kada prolazi kroz tačku x 2 \u003d 3. Dakle, x 2 \u003d 3 je minimalna tačka.

stranice, uz potpuno ili djelomično kopiranje materijala, obavezan je link na izvor.

Sa ovom uslugom možete pronaći najveću i najmanju vrijednost funkcije jedna varijabla f(x) sa dizajnom rješenja u Wordu. Ako je zadana funkcija f(x,y), potrebno je pronaći ekstremum funkcije dvije varijable. Također možete pronaći intervale povećanja i smanjenja funkcije.

Pravila unosa funkcije:

Neophodan uslov za ekstremum funkcije jedne varijable

Jednadžba f "0 (x *) \u003d 0 je neophodan uslov za ekstremum funkcije jedne varijable, tj. u tački x * prvi izvod funkcije mora nestati. Odabire stacionarne tačke x c ​​u kojima funkcija ne povećava se i ne smanjuje.

Dovoljan uslov za ekstremum funkcije jedne varijable

Neka je f 0 (x) dvaput diferencibilan u odnosu na x koji pripada skupu D . Ako je u tački x * ispunjen uslov:

F" 0 (x *) = 0
f"" 0 (x *) > 0

Tada je tačka x * tačka lokalnog (globalnog) minimuma funkcije.

Ako je u tački x * ispunjen uslov:

F" 0 (x *) = 0
f"" 0 (x *)< 0

Ta tačka x * je lokalni (globalni) maksimum.

Primjer #1. Pronađite najveću i najmanju vrijednost funkcije: na segmentu.
Rješenje.

Kritična tačka je jedan x 1 = 2 (f'(x)=0). Ova tačka pripada segmentu . (Tačka x=0 nije kritična, jer je 0∉).
Izračunavamo vrijednosti funkcije na krajevima segmenta i na kritičnoj tački.
f(1)=9, f(2)= 5 / 2 , f(3)=3 8 / 81
Odgovor: f min = 5 / 2 za x=2; f max =9 pri x=1

Primjer #2. Koristeći derivacije višeg reda, pronađite ekstremum funkcije y=x-2sin(x) .
Rješenje.
Pronađite izvod funkcije: y’=1-2cos(x) . Nađimo kritične tačke: 1-cos(x)=2, cos(x)=1, x=± π / 3 +2πk, k∈Z. Nalazimo y''=2sin(x), izračunajmo , pa su x= π / 3 +2πk, k∈Z minimalne tačke funkcije; , pa su x=- π / 3 +2πk, k∈Z maksimalne tačke funkcije.

Primjer #3. Istražiti funkciju ekstrema u okolini tačke x=0.
Rješenje. Ovdje je potrebno pronaći ekstreme funkcije. Ako je ekstrem x=0, onda saznajte njegov tip (minimum ili maksimum). Ako među pronađenim tačkama nema x = 0, onda izračunajte vrijednost funkcije f(x=0).
Treba napomenuti da kada derivacija na svakoj strani date tačke ne promijeni svoj predznak, moguće situacije nisu iscrpljene čak ni za diferencijabilne funkcije: može se dogoditi da za proizvoljno malo susjedstvo na jednoj strani tačke x 0 ili na obje strane derivacija mijenja predznak. U ovim tačkama, potrebno je primijeniti druge metode za proučavanje funkcija do ekstrema.

Primjer #4. Podijelite broj 49 na dva člana, čiji će proizvod biti najveći.
Rješenje. Neka je x prvi pojam. Tada je (49-x) drugi član.
Proizvod će biti maksimalan: x (49-x) → max

Tačka x 0 se zove maksimalni poen(minimum) funkcije f(h) ako je u nekoj okolini tačke x 0 ispunjena nejednakost f(h) ≤f(h 0) (f(h) ≥f(h 0)).

Vrijednost funkcije u ovoj tački se poziva u skladu s tim maksimum ili minimum funkcije. Maksimum i minimum funkcije su kombinovani zajedničkim imenom ekstrem funkcije.

Ekstremum funkcije u ovom smislu često se naziva lokalni ekstrem, naglašavajući činjenicu da je ovaj koncept povezan samo sa dovoljno malim susjedstvom tačke x 0 . Na istom intervalu, funkcija može imati nekoliko lokalnih maksimuma i minimuma, koji se ne poklapaju nužno sa globalni maksimum ili minimum(tj. najveća ili najmanja vrijednost funkcije na cijelom intervalu).

Neophodan uslov za ekstrem. Da bi funkcija u nekoj tački imala ekstrem, potrebno je da njen izvod u toj tački bude jednak nuli ili da ne postoji.

Za diferencijabilne funkcije ovaj uvjet slijedi iz Fermatove teoreme. Osim toga, predviđa slučaj kada funkcija ima ekstrem u točki u kojoj nije diferencibilna.

Pozivaju se tačke u kojima je zadovoljen uslov ekstrema kritičan(ili stacionarno za diferencijabilnu funkciju). Ove tačke moraju biti unutar opsega funkcije.

Dakle, ako postoji ekstremum u bilo kojoj tački, onda je ova tačka kritična (uslov potrebe). Imajte na umu da obrnuto nije tačno. Kritična tačka nije nužno tačka ekstrema, tj. navedeni uslov nije dovoljan.

Prvi dovoljan uslov za ekstrem. Ako pri prolasku kroz određenu tačku derivacija diferencijabilne funkcije promijeni svoj predznak s plusa na minus, onda je to maksimalna točka funkcije, a ako je od minusa do plusa, onda je minimalna točka.

Dokaz ovog uvjeta slijedi iz uvjeta dovoljne monotonosti (kada se promijeni predznak derivacije, dolazi do prijelaza ili iz povećanja funkcije u smanjenje, ili iz smanjenja u povećanje).

Drugi dovoljan uslov za ekstrem. Ako je prvi izvod duplo diferencibilne funkcije nula u nekoj tački, a drugi izvod pozitivan u toj tački, onda je ovo minimalna tačka funkcije; a ako je drugi izvod negativan, onda je ovo maksimalna tačka.

Dokaz ovog uslova je takođe zasnovan na uslovu dovoljne monotonosti. Zaista, ako je drugi izvod pozitivan, onda je prvi izvod rastuća funkcija. Pošto je u razmatranoj tački jednak nuli, pri prolasku kroz nju mijenja predznak iz minusa u plus, što nas vraća na prvi dovoljan uvjet za lokalni minimum. Slično, ako je drugi izvod negativan, tada prvi opada i mijenja predznak iz plusa u minus, što je dovoljan uvjet za lokalni maksimum.

Istraživanje funkcije do ekstrema u skladu sa formulisanim teoremama, uključuje sljedeće korake:

1. Pronađite prvi izvod funkcije f`(x).

2. Provjeriti ispunjenost potrebnog ekstremnog uslova, tj. pronaći kritične tačke funkcije f(x) u kojima izvod f`(x) = 0 ili ne postoji.

3. Provjeriti ispunjenost uslova dovoljnog ekstrema, tj. ili ispitajte predznak izvoda lijevo i desno od svake kritične tačke, ili pronađite drugi izvod f``(x) i odredite njegov predznak u svakoj kritičnoj tački. Donijeti zaključak o prisutnosti ekstrema funkcije.

4. Pronađite ekstreme (ekstremne vrijednosti) funkcije.

Pronalaženje globalnog maksimuma i minimuma funkcije na određenom intervalu je takođe od velike praktične važnosti. Rješenje ovog problema na segmentu zasniva se na Weierstrassovom teoremu, prema kojem kontinuirana funkcija uzima svoje maksimalne i minimalne vrijednosti na segmentu. Mogu se postići i na ekstremnim tačkama i na krajevima segmenta. Stoga rješenje uključuje sljedeće korake:

1. Pronađite izvod funkcije f`(x).

2. Naći kritične tačke funkcije f(x) u kojima izvod f`(x) = 0 ili ne postoji.

3. Pronađite vrijednosti funkcije na kritičnim tačkama i na krajevima segmenta i odaberite najveću i najmanju od njih.

Ovo je prilično zanimljiv dio matematike s kojim se susreću apsolutno svi diplomirani studenti i studenti. Međutim, ne vole svi matan. Neki ne razumiju čak ni osnovne stvari kao što je naizgled standardna studija funkcija. Ovaj članak ima za cilj da ispravi ovaj previd. Želite li saznati više o analizi funkcija? Želite li znati šta su ekstremne tačke i kako ih pronaći? Onda je ovaj članak za vas.

Istraživanje grafa funkcije

Za početak, vrijedi razumjeti zašto je uopće potrebno analizirati grafikon. Postoje jednostavne funkcije koje je lako nacrtati. Upečatljiv primjer takve funkcije je parabola. Nije teško nacrtati njen grafikon. Sve što je potrebno je jednostavnom transformacijom pronaći brojeve kod kojih funkcija poprima vrijednost 0. U principu, ovo je sve što trebate znati da biste nacrtali graf parabole.

Ali što ako je funkcija koju trebamo grafički prikazati mnogo složenija? Kako su svojstva složenih funkcija prilično neočigledna, potrebno je izvršiti cjelovitu analizu. Tek tada se funkcija može grafički prikazati. Kako uraditi? Odgovor na ovo pitanje možete pronaći u ovom članku.

Plan analize funkcija

Prvo što treba učiniti je izvršiti površno proučavanje funkcije, tokom kojeg ćemo pronaći domen definicije. Dakle, počnimo redom. Domen definicije je skup onih vrijednosti kojima je funkcija definirana. Jednostavno rečeno, ovo su brojevi koji se mogu koristiti u funkciji umjesto x. Da biste odredili obim, potrebno je samo pogledati zapisnik. Na primjer, očito je da funkcija y (x) \u003d x 3 + x 2 - x + 43 ima domenu definicije - skup realnih brojeva. Pa, sa funkcijom kao što je (x 2 - 2x) / x, sve je malo drugačije. Pošto broj u nazivniku ne bi trebao biti jednak 0, tada će domen ove funkcije biti svi realni brojevi, osim nule.

Zatim morate pronaći takozvane nule funkcije. Ovo su vrijednosti argumenta za koje cijela funkcija uzima vrijednost nulu. Da biste to učinili, potrebno je izjednačiti funkciju s nulom, detaljno je razmotriti i izvršiti neke transformacije. Uzmimo već poznatu funkciju y(x) = (x 2 - 2x)/x. Iz školskog predmeta znamo da je razlomak 0 kada je brojilac nula. Stoga odbacujemo nazivnik i počinjemo raditi s brojnikom, izjednačavajući ga sa nulom. Dobijamo x 2 - 2x \u003d 0 i izvadimo x iz zagrada. Dakle, x (x - 2) = 0. Kao rezultat, nalazimo da je naša funkcija jednaka nuli kada je x jednako 0 ili 2.

Tokom proučavanja grafa funkcije, mnogi se suočavaju s problemom u obliku ekstremnih tačaka. I to je čudno. Uostalom, ekstremi su prilično jednostavna tema. Ne vjerujete? Uvjerite se i sami čitajući ovaj dio članka, u kojem ćemo govoriti o minimalnim i maksimalnim bodovima.

Za početak, vrijedi razumjeti šta je ekstrem. Ekstremum je granična vrijednost koju funkcija doseže na grafu. Iz ovoga ispada da postoje dvije ekstremne vrijednosti - maksimum i minimum. Radi jasnoće, možete pogledati gornju sliku. Na istraživanom području, tačka -1 je maksimum funkcije y (x) = x 5 - 5x, a tačka 1 je minimum.

Takođe, nemojte miješati pojmove jedni s drugima. Ekstremne tačke funkcije su oni argumenti u kojima data funkcija dobija ekstremne vrednosti. Zauzvrat, ekstrem je vrijednost minimuma i maksimuma funkcije. Na primjer, ponovo razmotrite gornju sliku. -1 i 1 su tačke ekstrema funkcije, a 4 i -4 su sami ekstremi.

Pronalaženje ekstremnih tačaka

Ali kako pronaći ekstremne tačke funkcije? Sve je prilično jednostavno. Prvo što treba učiniti je pronaći derivaciju jednačine. Recimo da smo dobili zadatak: "Pronađi tačke ekstrema funkcije y (x), x je argument. Radi jasnoće, uzmimo funkciju y (x) = x 3 + 2x 2 + x + 54. Razlikujemo i dobijemo sljedeću jednačinu: 3x 2 + 4x + 1. Kao rezultat, dobili smo standardnu ​​kvadratnu jednačinu. Sve što treba uraditi je da je izjednačimo sa nulom i pronađemo korijene. Pošto je diskriminanta veća od nule (D \u003d 16 - 12 \u003d 4), ova jednadžba je određena sa dva korijena. Pronalazimo ih i dobivamo dvije vrijednosti: 1/3 i -1. Ovo će biti tačke ekstrema funkcije. Međutim, kako još uvijek možete odrediti ko je ko? Koja tačka je maksimum, a koja minimum? Da biste to učinili, morate uzeti susjednu tačku i saznati njenu vrijednost. Na primjer, uzmimo broj -2, koji je lijevo duž koordinate liniju od -1 Ovu vrijednost zamjenjujemo u našu jednačinu y (-2) = 12 - 8 + 1 = 5. Kao rezultat, dobili smo pozitivan broj.To znači da na intervalu od 1/3 do -1 funkcija raste, što zauzvrat znači da se na intervalima od minus beskonačnosti do 1/3 i od -1 do plus beskonačnosti funkcija smanjuje. Dakle, možemo zaključiti da je broj 1/3 minimalna tačka funkcije na ispitivanom intervalu, a -1 tačka maksimuma.

Također je vrijedno napomenuti da ispit zahtijeva ne samo pronalaženje ekstremnih bodova, već i izvođenje neke vrste operacije s njima (zbrajanje, množenje, itd.). Iz tog razloga vrijedi obratiti posebnu pažnju na uslove problema. Uostalom, zbog nepažnje možete izgubiti bodove.

Razmotrimo graf neprekidne funkcije y=f(x) prikazano na slici.

Vrijednost funkcije u tački x 1 će biti veći od vrijednosti funkcije u svim susjednim točkama i lijevo i desno od x 1 . U ovom slučaju se kaže da funkcija ima u tački x 1 max. U tački x Funkcija 3 očito također ima maksimum. Ako uzmemo u obzir poentu x 2, tada je vrijednost funkcije u njemu manja od svih susjednih vrijednosti. U ovom slučaju se kaže da funkcija ima u tački x 2 minimum. Slično za poentu x 4 .

Funkcija y=f(x) u tački x 0 ima maksimum, ako je vrijednost funkcije u ovoj tački veća od njenih vrijednosti u svim točkama nekog intervala koji sadrži točku x 0 , tj. ako postoji takva okolina tačke x 0, što je za svakoga x≠x 0 , koji pripada ovoj četvrti, imamo nejednakost f(x)<f(x 0 ) .

Funkcija y=f(x) Ima minimum u tački x 0 , ako postoji takva okolina tačke x 0 , šta je za svakoga x≠x 0 koji pripada ovoj četvrti, imamo nejednakost f(x)>f(x0.

Tačke u kojima funkcija doseže svoj maksimum i minimum nazivaju se točke ekstrema, a vrijednosti funkcije u tim točkama su ekstremi funkcije.

Obratimo pažnju na činjenicu da funkcija definisana na segmentu može dostići svoj maksimum i minimum samo u tačkama koje se nalaze unutar segmenta koji se razmatra.

Imajte na umu da ako funkcija ima maksimum u nekoj tački, to ne znači da u ovom trenutku funkcija ima maksimalnu vrijednost u cijeloj domeni. Na gornjoj slici, funkcija u tački x 1 ima maksimum, iako postoje tačke u kojima su vrijednosti funkcije veće nego u tački x 1 . posebno, f(x 1) < f(x 4) tj. minimum funkcije je veći od maksimuma. Iz definicije maksimuma samo slijedi da je to najveća vrijednost funkcije u tačkama koje su dovoljno blizu tačke maksimuma.

Teorema 1. (Neophodan uslov za postojanje ekstrema.) Ako je diferencijabilna funkcija y=f(x) ima u tački x= x 0 ekstremu, onda njegov izvod u ovoj tački nestaje.

Dokaz. Neka, radi određenosti, u tački x 0 funkcija ima maksimum. Zatim za dovoljno male inkremente Δ x imamo f(x 0 + Δ x) 0 ) , tj. Ali onda

Prenoseći ove nejednakosti do granice kao Δ x→ 0 i uzimajući u obzir da je izvod f "(x 0) postoji, pa stoga granica na lijevoj strani ne ovisi o tome kako Δ x→ 0, dobijamo: za Δ x → 0 – 0 f"(x 0) ≥ 0 i na Δ x → 0 + 0 f"(x 0) ≤ 0. Pošto f"(x 0) definira broj, onda su ove dvije nejednakosti kompatibilne samo ako f"(x 0) = 0.

Dokazana teorema kaže da maksimum i minimum točke mogu biti samo među onim vrijednostima argumenta za koje derivacija nestaje.

Razmotrili smo slučaj kada funkcija ima derivaciju u svim tačkama određenog segmenta. Šta se dešava kada izvod ne postoji? Razmotrite primjere.

Primjeri.

1. y=|x|.

   Funkcija nema izvod u tački x=0 (u ovom trenutku graf funkcije nema definitivnu tangentu), ali u ovom trenutku funkcija ima minimum, jer y(0)=0, i za sve x≠ 0y > 0.



Funkcija nema izvod at x=0, pošto ide u beskonačnost kada x=0. Ali u ovom trenutku funkcija ima maksimum.



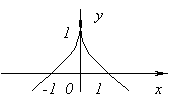
Funkcija nema izvod at x=0 jer at x→0. U ovom trenutku funkcija nema ni maksimum ni minimum. stvarno, f(x)=0 i at x<0f(x)<0, а при x>0f(x)>0.



Dakle, iz datih primera i formulisane teoreme jasno je da funkcija može imati ekstrem samo u dva slučaja: 1) u tačkama gde izvod postoji i jednak je nuli; 2) u tački u kojoj izvod ne postoji.

Međutim, ako u nekom trenutku x 0 mi to znamo f"(x 0 ) =0, onda se iz ovoga ne može zaključiti da je u tački x 0 funkcija ima ekstrem.

Na primjer. .



Ali poenta x=0 nije tačka ekstrema, jer se lijevo od ove tačke vrijednosti funkcije nalaze ispod ose Ox, i iznad desno.

Vrijednosti argumenta iz domene funkcije, za koje derivacija funkcije nestaje ili ne postoji, nazivaju se kritične tačke.




Iz prethodnog proizilazi da su tačke ekstrema funkcije među kritičnim tačkama, ali, međutim, nije svaka kritična tačka tačka ekstrema. Stoga, da biste pronašli ekstremu funkcije, morate pronaći sve kritične točke funkcije, a zatim ispitati svaku od ovih tačaka zasebno za maksimum i minimum. Za to služi sljedeća teorema.

Teorema 2. (dovoljan uslov za postojanje ekstremuma.) Neka je funkcija kontinuirana na nekom intervalu koji sadrži kritičnu tačku x 0 , i diferencibilan je u svim tačkama ovog intervala (osim, možda, same tačke x 0). Ako pri prolasku s lijeva na desno kroz ovu tačku derivacija promijeni predznak sa plusa na minus, tada u tački x = x 0 funkcija ima maksimum. Ako, prilikom prolaska x 0 s lijeva na desno, derivacija mijenja predznak iz minusa u plus, tada funkcija ima minimum u ovoj tački.

Dakle, ako

Dokaz. Pretpostavimo prvo da kada prolazimo x 0, derivacija mijenja predznak iz plusa u minus, tj. za sve x blizu tačke x 0 f "(x)> 0 for x< x 0 , f"(x)< 0 for x > x 0 . Primijenimo Lagrangeov teorem na razliku f(x) - f(x 0 ) = f "(c)(x- x 0), gdje c leži između x I x 0 .

1. Neka x< x 0 . Onda c< x 0 i f "(c)> 0. Zbog toga f "(c)(x-x 0)< 0 i, prema tome,

   f(x) - f(x 0 )< 0, tj. f(x)< f(x 0 ).

2. Neka x > x 0 . Onda c>x 0 i f"(c)< 0. Sredstva f "(c)(x-x 0)< 0. Zbog toga f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .

Dakle, za sve vrijednosti x dovoljno blizu x 0 f(x)< f(x 0 ) . A to znači da u ovom trenutku x 0 funkcija ima maksimum.

Slično se dokazuje i drugi dio minimalne teoreme.



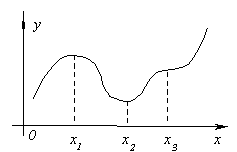
Ilustrujmo značenje ove teoreme na slici. Neka f"(x 1 ) =0 i za bilo koje x, dovoljno blizu x 1, nejednakosti

f"(x)< 0 at x< x 1 , f "(x)> 0 at x > x 1 .

Zatim lijevo od tačke x 1 funkcija raste, a desno opada, dakle, kada x = x 1 funkcija ide od povećanja ka opadajućoj, odnosno ima maksimum.

Slično, mogu se razmotriti tačke x 2 i x 3 .


Šematski se sve navedeno može prikazati na slici:

Pravilo za proučavanje funkcije y=f(x) za ekstrem

1. Pronađite opseg funkcije f(x).
2. Pronađite prvi izvod funkcije f"(x).
3. Odredite kritične tačke, za ovo:
   1. pronađite prave korijene jednačine f"(x)=0;
   2. pronađite sve vrijednosti x pod kojim derivat f"(x) ne postoji.
4. Odredite predznak derivacije lijevo i desno od kritične tačke. Pošto predznak izvoda ostaje konstantan između dvije kritične tačke, dovoljno je odrediti predznak izvoda u bilo kojoj tački lijevo i u jednoj tački desno od kritične tačke.
5. Izračunajte vrijednost funkcije u tačkama ekstrema.

Primjeri. Istražite funkcije za minimum i maksimum.




NAJVEĆE I MINIMALNE VRIJEDNOSTI FUNKCIJE NA PRESETKU

najveća vrijednost funkcije na segmentu je najveća od svih njenih vrijednosti na ovom segmentu, i najmanje je najmanja od svih njegovih vrijednosti.

Razmotrite funkciju y=f(x) kontinuirano na segmentu [ a, b]. Kao što je poznato, takva funkcija dostiže svoje maksimalne i minimalne vrijednosti, bilo na granici segmenta, bilo unutar njega. Ako je maksimalna ili minimalna vrijednost funkcije dostignuta u unutrašnjoj tački segmenta, tada je ta vrijednost maksimalna ili minimalna vrijednost funkcije, odnosno dostiže se u kritičnim tačkama.

Tako dobijamo sledeće pravilo za pronalaženje najveće i najmanje vrijednosti funkcije na segmentu [ a, b] :

1. Pronađite sve kritične tačke funkcije u intervalu ( a, b) i izračunajte vrijednosti funkcije u tim točkama.
2. Izračunajte vrijednosti funkcije na krajevima segmenta za x=a, x=b.
3. Od svih dobijenih vrijednosti odaberite najveću i najmanju.